Under normal situations, the usefulness of money doesn’t scale linearly. The more dollars you have, the less each additional dollar is worth it for you. If you initially have $100K and then you suddenly gain another $100K, for a total of $200K, this is a BIG DEAL. Doubling your money will really enhance your quality of life. But if instead you had $1M before that, then the additional $100K would bump you to $1.1M which is likely a much less significant change in quality of life.
That idea is often circulated in economics textbooks and popular literature. According to them the utility function of money is concave, meaning that each additional dollar provides less and less utility, fun or gusto.
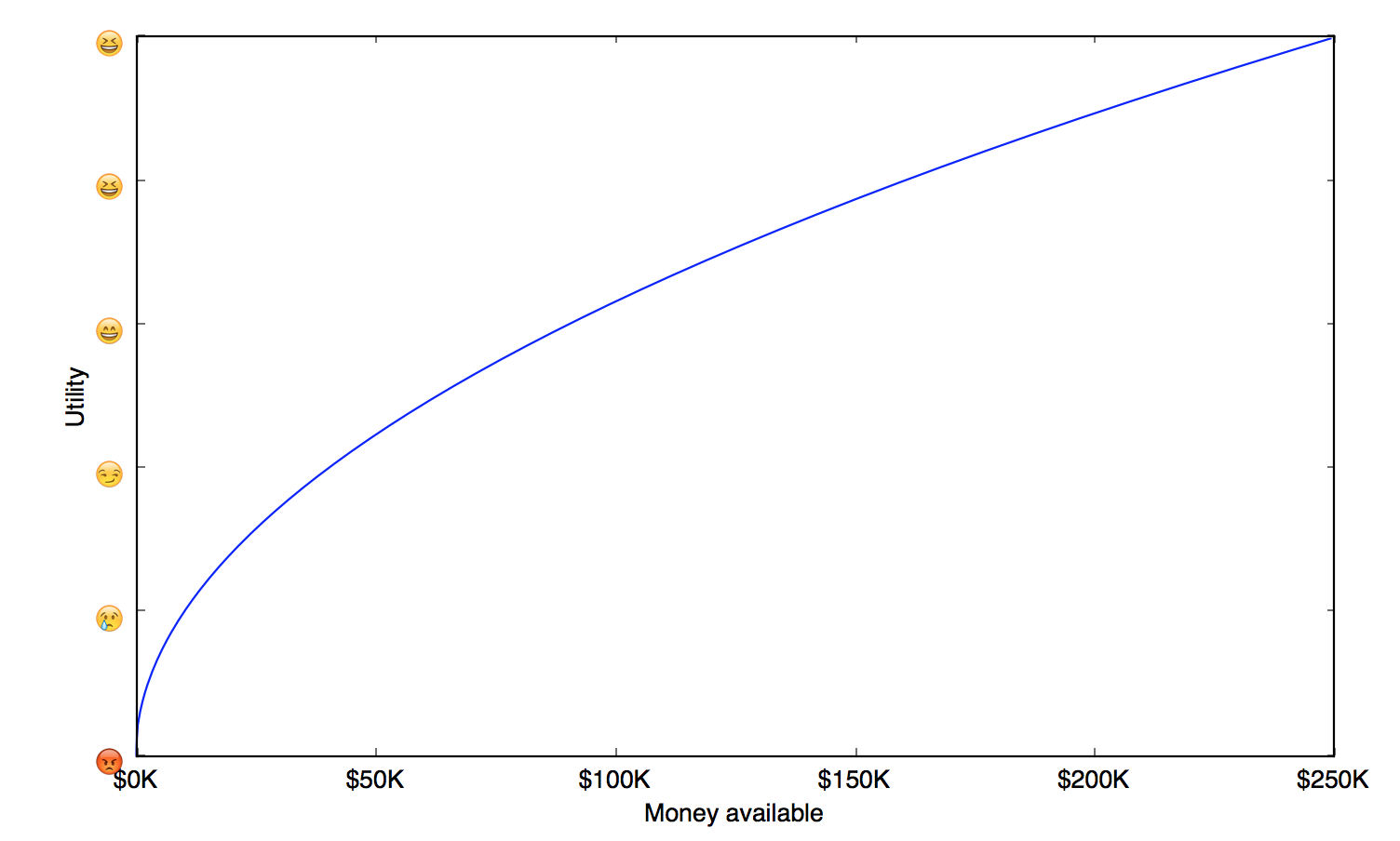
While this makes sense, it is a simplification of the reality. Simplifications are great, because they allow us to reason about “what-if” situation, ignoring most of the details.
But with utility of money, this simplification is misleading. Assuming that for every person, in every situation, money has concave utility, will lead to wrong predictions about what these people will do. Not only that, but it will lead to wrong advice, which can be dangerous and reckless.
In real life, each of us has options. Money enables options. There are certain actions that are impossible to do unless you have a certain amount of money. And each option has certain utility. If there was only one option available, then your utility function of money would be a step function. You either have the money to afford the option, or not.
Therefore, the utility function for money for every person is step-wise function. Yes, it is true that looked from a far, it might look concave. But if you look closely, you will notice that it has sections of flatness and then sudden jumps. Like a stairway to heaven…
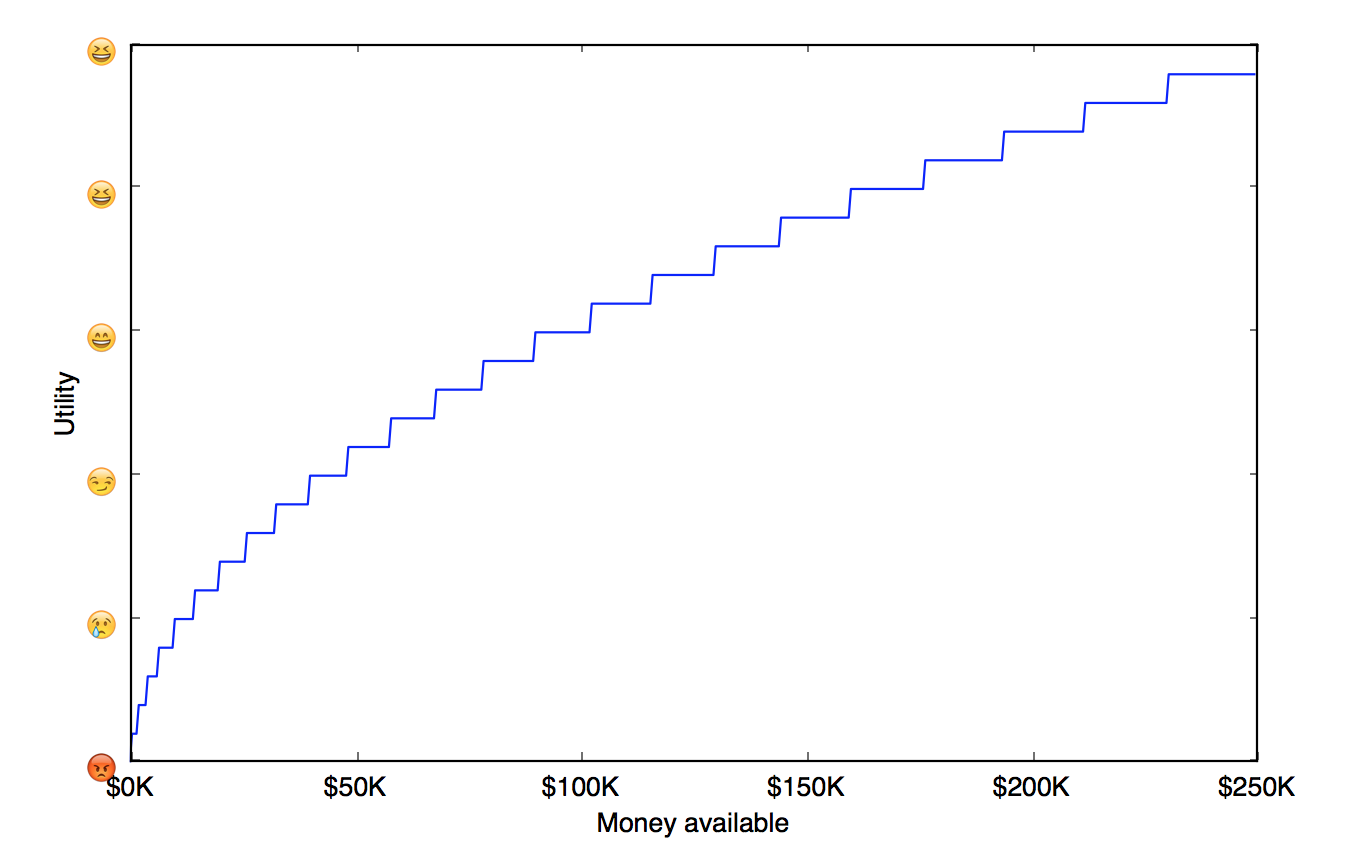
Lets revisit the example from the previous essay. A medical operation which is likely to cure you from a deadly disease might cost $200K. If you are unlucky enough to have that disease, then this option has a great utility to you.
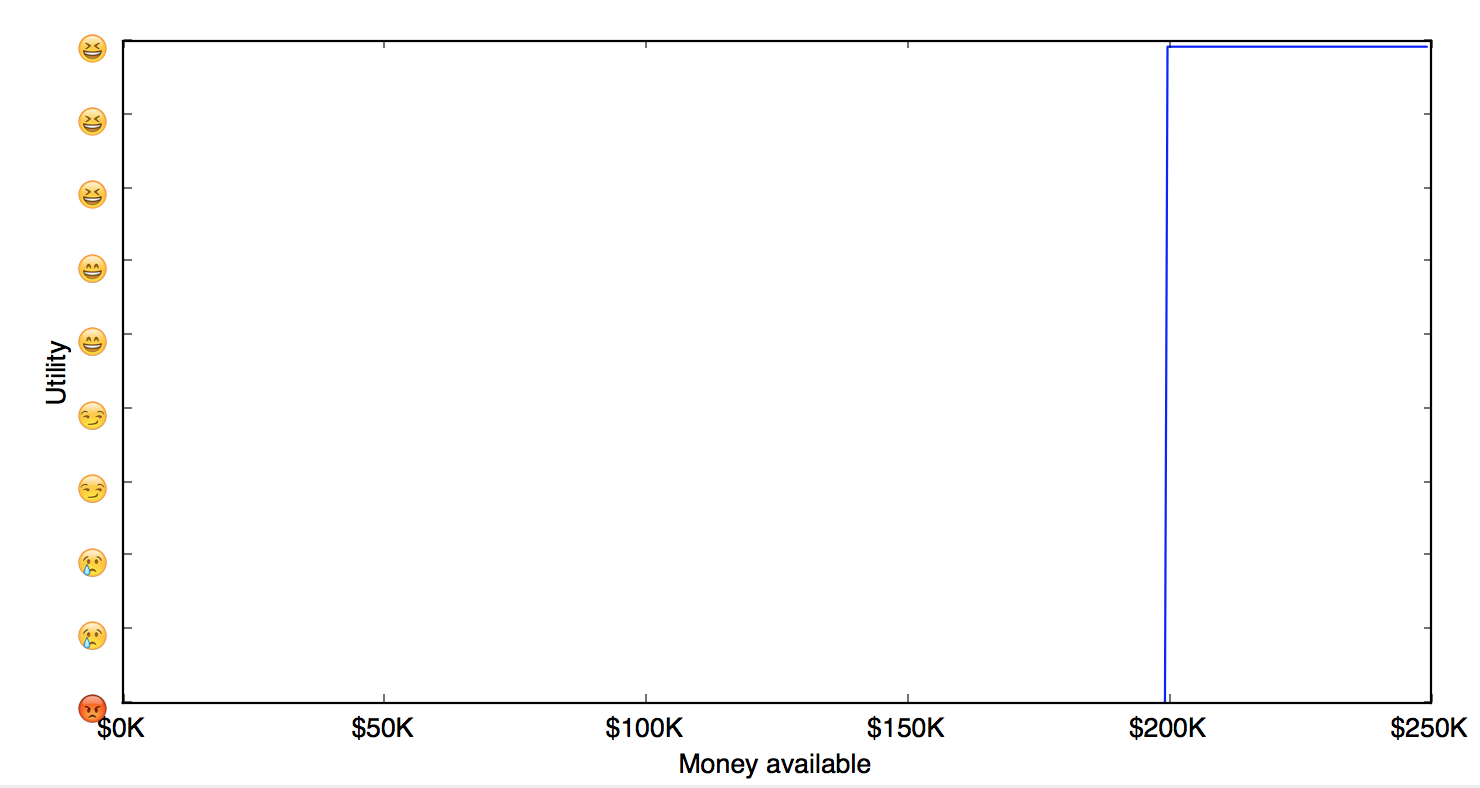
In such case, if you had $100K and gambling was legal, then you can gamble your money on roulette, and potentially win a chance to undergo that operation. In this case, gambling will give you approximately 43% chance of survival, so in reality your expected utility is positive.
This provides a little bit of detail about why it might make sense to gamble in this case… that is if you buy my arguments about the step function and if you buy into the concept of utility.
Now, here is the twist. I actually don’t agree that there is a single scalar utility function to desribe our preferences in life. It is a neat mathematical concept but deriving its existence requires us to make assumptions about human nature which are not true. The stairway to heaven metaphor is nice for our imagination, and thinking, and is strictly more accurate than the smooth concave model of utility.
Eventually, as we dig deeper, it will be imprecise and we’ll switch to a more accurate, but less neat model of preference.
But lets leave that discussion for the future essays. I am first going to discuss the stairway model in some practical examples.